Intro
A matrix is an array of numbers. They’re typically written in square brackets and look like this: 
If you’re not familiar with matrices and their addition and multiplication, take some time to get a bit used to them and come back once you’re ready.
A quick reminder, if I take matrix A then I multiply it by matrix B, I am doing the operation BA, which is not always the same as doing AB. Order is very important when multiplying matrices. The reason we read from right to left is convention, similarly to functions and the way we read f(g(x)) as applying g then applying f.
So if we can multiply matrices, is there a matrix that when multiplied does nothing? Indeed so, it is called the identity matrix. The way I think of it, the identity matrix is to matrix multiplication as multiplying by 1 is to normal multiplication and as adding by 0 is to doing addition. They all do nothing. But it’s an important concept because it helps you inverse things.
Say I multiplied by 2, and then realised it was an error, what must I multiply by to undo the 2, or what is the inverse of 2 when multiplying? It is ½. and notice that because 2×1=2, 2×½ = 1. When I multiply by two then by a half it is the same thing as doing nothing, or time-sing by 1. 2 and ½ are inverses of each other. And applying two inverse functions to each other must equal the identity.
Say I added by 2 and wanted to undo it. What do I need to do to inverse this addition by 2? I add by -2. and 2 + -2 = 0. Its the same as doing nothing.
So this is the 2×2 identity matrix:
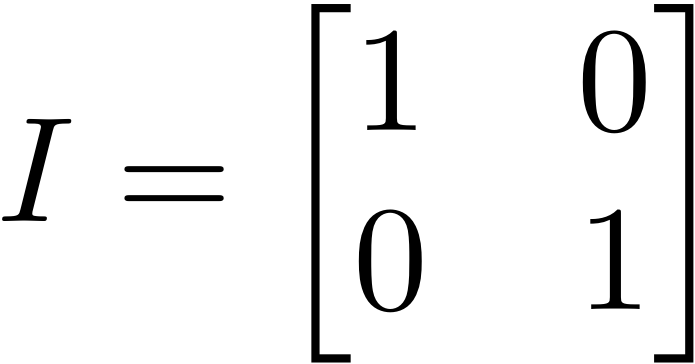
Memorise it and love it.
So just like multiplication of 2 by 1 will always result in 2, so will the multiplication of any matrix by the identity matrix (provided they can be multiplied) give the same matrix again. Lets call this general matrix M, and this identity matrix I. A property of the identity matrix is that MI=M and IM=M. The identity matrix is everywhere.
Lets expand on the concept of the inverse of a function. Just like 2×½ = 1, for some matrices there are matrices that when multiplied give the identity matrix. Lets phrase that using letters. If I have a matrix A and a matrix B, that when I multiply them give me I, then A must be the inverse of B, or B-1. B must also be A-1.
Now I wonder if there’s a formula that would conveniently give me the inverse of any matrix I wish (provided we’re not dividing by zero). Oh yeah there is! If you’ve studied matrices before this might have been one of the formulas you had drilled into you. It might have seemed abstract or as if it was pulled out of thin air. Lets remove that illusion and derive it ourselves.
Where we start proving things!
I would like to encourage you to not read on until you have proved it yourself. Spend a few minutes to a few months (depending on what you can bear) trying to prove the inverse matrix. Once you’ve got your proof done, come back and see how similar it was to mine. I’d rather not rob you of the satisfaction of finding something out for yourself.
So lets use M and M-1 to represent the general matrix, and the general matrix’s inverse.
Let
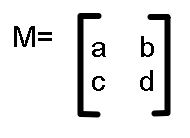
and
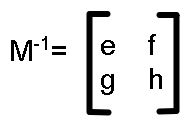
M-1M=I
So lets write that out in the equation.
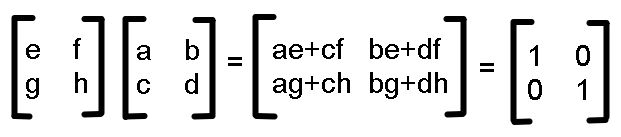
Yay simultaneous equations! We’re trying to phrase M-1 in terms of M. So my strategy from here will be to write each equation out twice, each time solving for a letter from e to h, then equating these equations to find out what each of e to h are in terms of a to d.
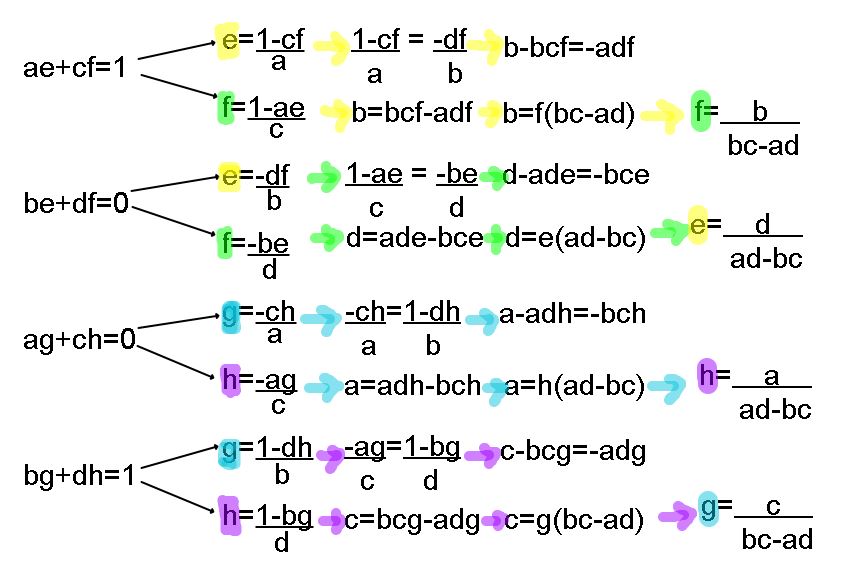
Wowwww there’s the determinant on the denominator! If you don’t know, the determinant of a matrix is the area formed by the parallelogram of the transformed unit square when applying a matrix transformation, it is equal to ad-bc which is a fun thing to prove. Another fun fact, I’ve spent years thinking it’s called determinat only to find out I was missing an n. A final fact, if your determinant equals 0 the inverse matrix is undefined because division by 0.
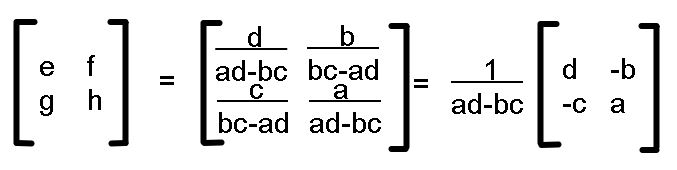
Voila! I hope you’ve enjoyed this proof. If you’d like any more proofs to do with linear transformations or maths and physics in general, dm us on instagram: @mathemattersblog and follow us as well for updates every time we post!
Photo by Rebecca Oliver on Unsplash
